Algorithmically Speaking - #2: A Game of Stones

This is the summary version of the article published in the Algorithmically Speaking newsletter which is only dedicated to exploring some of the most beautiful algorithmic problems and solutions in the history of Computer Science.

You can read the complete version by clicking on this link.

---

Hello there!

Today we are going to be diving into games and some of the mathematical theories behind them.

A simple game of stones will be the perfect excuse for me to let you know about general Game Theory and Graphs.

Let’s begin!

---

Formulating the Problem

In its simplest terms, the problem can be formulated as follows:

Let’s say there’s a heap of N stones. Players A and B move alternately, and player A begins. On each move, the player has to remove 1, 2, or 3 stones from the heap, and the player who removes the last stone wins the game. Given the initial number of stones N, which player will win if both of them play optimally?

As an example, let’s say the game starts with N = 5 stones. A possible outcome of the game could be the following:

1. Player A removes 1 stone. Leaves 4 stones on the heap.

2. Player B removes 2 stones. Leaves 2 stones on the heap.

3. Player A removes 2 stones. Leaves 0 stones on the heap and wins the game.

Another possible outcome could have been:

1. Player A removes 2 stones. Leaves 3 stones on the heap.

2. Player B removes 3 stones. Leaves 0 stones on the heap and wins the game.

In the first example, player A wins. In the second, player A loses. Which is probably more accurate than saying “Player B wins“. It all has to do with what are probably the most important words in the problem statement:

Both players play optimally

Let’s see what this means!

What it means to play Optimally

Analyzing the previous game we can see that there is no randomness in it both players have the same set of moves and they take turns to play.

Intuitively, it makes sense that the first player has some type of advantage, and here is where the words “to play optimally“ make sense.

Essentially, it means that if there is a chance for a player to make a move that will guarantee its victory, the player will make that move (or another one that also guarantees victory). And, of course, it also means that the only way a player will lose is if a move that can guarantee its victory doesn’t exist at any time.

Taking this into account, the second sample outcome shown above could never happen. Player A won’t make a move that will result in an eventual loss if it has the option to make a move that will guarantee victory. The first sample outcome is an example of that. Let’s see why:

1. Player A takes 1 stone. Leaves 4 stones on the heap.

2. The options that Player B has to play are to remove 1, 2, or 3 stones from the heap. This would leave the heap with 3, 2, or 1 stone left, respectively.

3. In any case, Player A can take all remaining stones and win the game.

So, it is inevitable for Player A to win if it makes the correct first move. If we simulate the first few instances of this game by hand we could determine if the first player will win or lose, depending on the initial size of the heap (try to do this as an exercise):

0 1 2 3 4 5 6 7 8 9
L W W W L W W W L W

By simple inspection, it looks like if the heap has a size that is a multiple of 4, the first player will lose. Otherwise, it will win.

Let’s see how to calculate this automatically.

Winning and Losing States

This game can be characterized by “states“ representing the current size of the heap. If we initially have a heap of size N, we have one state for every heap size from 0 to N.

Let’s define a winning state as a state where the player can make a move and leave the opponent player in a losing state. Conversely, a losing state is such a state in which every possible move will leave the opponent player in a winning state.

For example, in our previous game, states 1, 2, and 3 are winning states because we can select 1, 2, or 3 stones respectively, and leave our opponent with a heap of 0 stones.

The state corresponding to a heap with 4 stones is a losing state because, no matter how many stones the player removes it will leave the opponent player with either 1, 2, or 3 stones, which corresponds to winning states.

Then, the state corresponding to a heap of size 5 is a winning state because we can remove 1 stone and leave our opponent playing in a heap with 4 stones, which is a losing state. And so on…

If we were to create a program that calculates winning and losing states for this game we could do something like this:

def calculate(N):
    winning = [False for _ in range(N + 1)]
    moves = [1, 2, 3]
    for state in range(1, N + 1):
        for move in moves:
            next_state = state - move
            if next_state >= 0 and not winning[next_state]:
                winning[state] = True
    return winning

The previous function returns a list with a boolean value for every state:

• True means that the state is a winning state and that the starting player can win the game if he plays optimally.

• False means that the state is a losing state and that the starting player cannot win the game no matter what move he plays if the opponent plays optimally.

What we have in our hands is an algorithm that can tell us if it’s worth playing this game. We can beat our opponents for sure or respectfully decline to play, depending on the heap size.

Let’s see how to generalize the previous algorithm for it to work for other games.

The State Graph

The characterization of these types of games into states is most commonly represented as a graph where states are the nodes and the edges between the nodes are defined by the available moves in every state.

For a heap of 5 stones in the previous game, we have the following state graph:

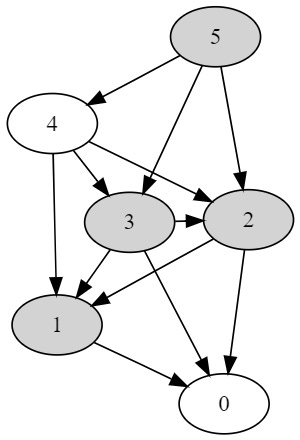
The state graph for N = 5.

Filled nodes represent winning states, and blank nodes represent losing states. The edges of the graphs determine the fact that we can transition from one state to another by making one of the available moves (in this case, removing 1, 2, or 3 stones).

Notice the fact that the resulting graph is a Directed Acyclic Graph. Every time we can characterize our game into a set of states and a group of moves that lead from one state to another, and that graph doesn’t contain cycles we can create an algorithm like the following for calculating winning and losing states:

def is_winning(state):
    moves = get_moves(state)
    for move in moves:
        next_state = get_next(state, move)
        if not is_winning(next_state):
            return True
    return False

The previous algorithm is like a template for calculating winning and losing positions in a state graph that is both directed and acyclic. For every specific game, the concepts of state, move, and transition will vary. But the principles shown in this post will be similar.

Also, this algorithm can be optimized using some Dynamic Programming techniques. I will leave that as a task for you to investigate. But don’t worry, I will be covering this in future posts.

Conclusions

I hope I was able to ignite your passion for Game Theory and Graphs by driving you through one of the most interesting topics in the history of Computer Science.

Some takeaways:

• Some games can be characterized as a set of states, moves, and transitions between the states.

• This characterization is known as a State Graph.

• The ability to determine winning and losing states beforehand can be the difference between scoring a safe win or an inevitable loss.

• Pro Tip: If you are playing against a human opponent and you have to make a move in a losing state, don’t lose hope. Try to go for the move that will make you lose in the maximum amount of turns and hope your opponent will make a mistake. Remember, all this theory works if they know how to play optimally 😉. Most people don’t.

I wish you good luck when solving this week’s challenges. Don’t forget to share your progress with the community!

And if you think this post can be helpful for someone, share it with them. Nothing will make me happier!

See you next week!

---

👋 Hello, I'm Alberto, Software Developer at doWhile, Competitive Programmer, Teacher, and Fitness Enthusiast.

🧡 If you liked this article, consider sharing it.

🔗 All links | Twitter | LinkedIn